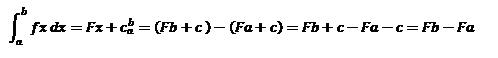Los pasos para el Teorema fundamental del cálculo

1.-Se verifica el dominio de la función de la integral dentro del intervalo a evaluar. ( el teorema sólo se puede aplicar si la función es continua para todo el intervalo.)

2.- Se resuelve la integral de acuerdo a la función presente, puede ser cualquier método de integración. ( los límites de integración deben concondar con la variable a estudiar, es decir si se realiza un cambio de variable se deben cambiar los límites)

3.- Se debe evaluar la función resultante, sustituyendo los límites  superior menos inferior, como se puede ver en la fugura es por la diferencia.

Propiedades de la integral definida:

La constante de integración no se coloca en la integrales definidas porque ellas se anulan por ser la diferncia entre los límites.

Ejemplo: